Node Weighted Steiner Tree

• INSTANCE: Graph 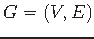$G=(V,E)$ , set of terminals 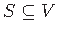$S\subseteq V$ and a node weight function $w : V \rightarrow \mathbb{R}^+$ .
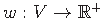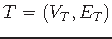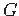• SOLUTION: A tree $T=(V_{T}, E_{T})$ in $G$ , such that $S \subseteq V_{T} \subseteq V$ , $E_{T} \subseteq E$ .
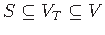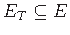• COST FUNCTION: $\sum_{v \in V_{T}}w(v)$
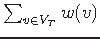
• OBJECTIVE: Minimize.
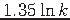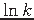• Approx.: Approximable within approximation ratio $1.35 \ln k$ [54]. Approximable within approximation ratio $\ln k$ in the unweighted case [54]. The online version admits a polynomial time poly-logarithmic competitive online algorithm [91].
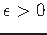• Hardness: NP-Hard [90],[40]. NP-hard to approximate within $(1-\epsilon )\ln (k)$ for every $\epsilon >0$ [54].
• Comment: Node Weighted Steiner Tree in Unit Disk Graphs is approximable within approximation ratio 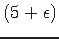$(5+ \epsilon)$ . Admits a PTAS for the special case when the set of vertices is c-local.
  A set of vertices 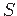$S$ is called c-local in a node weighted graph if in the minimum node weighted spanning tree for S, the weight of longest edge is at most c [84].