

Next: Terminal Steiner Tree
Up: Steiner Tree Problems
Previous: Euclidean Steiner Tree Problem
- INSTANCE:
Graph
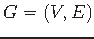 , set of terminals
, set of terminals
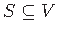 such that each
such that each 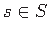 has at least
has at least
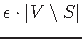 neighbors in
neighbors in
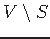
- SOLUTION:
A Steiner tree
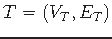 for
for 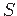 in
in 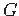
- COST FUNCTION:
length
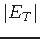 of
of 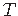
- OBJECTIVE:
Minimize
- Approx.:
For every
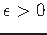 , there exists a PTAS for the
, there exists a PTAS for the 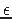 -Dense Steiner Tree Problem
[74]. This also yields existence of an efficient PTAS [64]).
The
-Dense Steiner Tree Problem
[74]. This also yields existence of an efficient PTAS [64]).
The 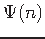 -Subdense Steiner Tree Problem where every terminal has at least
-Subdense Steiner Tree Problem where every terminal has at least
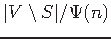 non-terminal
neighbors also admits a PTAS for
non-terminal
neighbors also admits a PTAS for
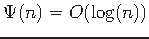 [25].
[25].
- Comment:
So far the problem is not known to be NP-hard in the exact setting.
2015-04-27 Revision: 288 PDF version