

Next: Internal Steiner Tree
Up: Steiner Tree Problems
Previous: -Dense Steiner Tree Problem
- INSTANCE:
Graph
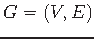 , cost function
, cost function
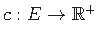 , set of terminals
, set of terminals
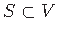 .
.
- SOLUTION:
A tree
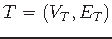 in
in 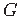 such that
such that
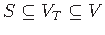 ,
,
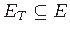 and
and
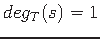 for every
for every 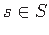 .
.
- COST FUNCTION:
 .
.
- OBJECTIVE:
Minimize.
be approximated within a factor less than
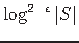 . This bound also applies to the node-weighted case. [16]
. This bound also applies to the node-weighted case. [16]
- Approx.:
Approximable within approximation ratio 2.458 on metric instances [33]. Can be improved to 1.9329 using the algorithm presented in [21].
- Comment:
For the special case of unit disc graphs, a 20-approximation was given by Biniaz et al. [15]. For the euclidean bottleneck version of this problem, an exact solution can be computed in polynomial time [14].
2015-04-27 Revision: 288 PDF version